You are here: OGC Public Wiki>HydrologyDWG Web>GroundwaterInteroperabilityExperiment2>29Jan2015--GW2IEMeeting30>AquiferTestingDiscussion (24 Feb 2015, EricBoisvert)Edit Attach
Aquifer Testing Discussion
We tried to see if we could implement the aquifer test (or pump test) in a pure O&M encoding. There are several requirements that need to be considered- Test can involve more than one Well/Bore
- Test generate intermediate data (drawdown curves) from which other parameters are derived
- Some data are related to the process itself (discharge of the pump, interval of the test)
- The parameters that are infered from the test must be somehow related to GW_UnitFluidProperty, which is itself an association between a unit and the fluid body
- aquifertesting.png:
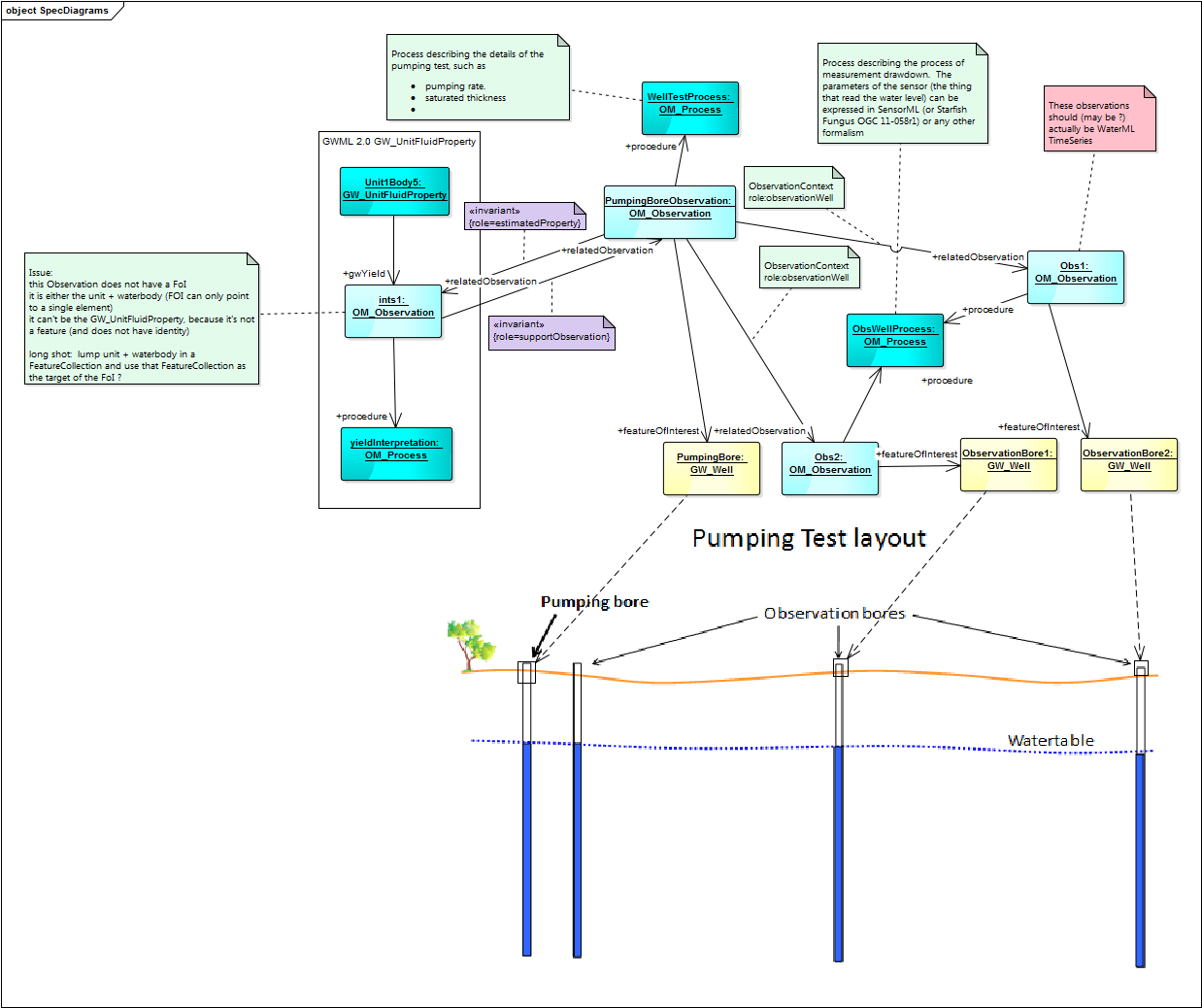
| Model | Pro | Con |
| SensorML | formal, no need to develop something | complex |
| *FL | eleguant approach (ex-factory + dynamic) | not standard, about Sensor (bit streched) - see below |
| NamedValue | Simple | ad hoc overload of Observation parameters |
| Custom (develop our own) | No ambiguity, more constrained semantic | world of its own that it might be futile to attemp to define every possible cases |
- Aquifer Test:

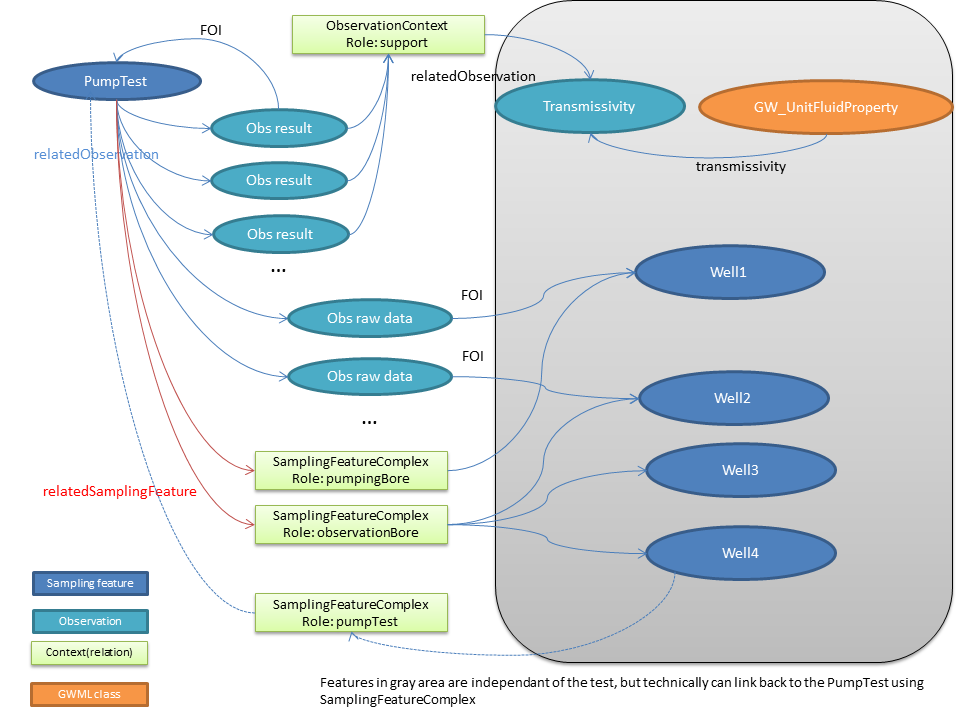 -- EricBoisvert - 24 Feb 2015
-- EricBoisvert - 24 Feb 2015
Pump
Although "Pump" is an important part of the aquifer test, the real piece of information is the pumping (rate, method, etc..), not the device because there is a difference between a device capacity and its actual performance once used. When a device need to be documented, it's when it's part of the construction because we might be interested in its range of use. *FL (Starfish Fungus Language - OGC 11-058r1) proposed two way to document a Sensor (but it could be extended to a device)- Its ex characteristic (parameter provider by the manifacturer)
- Its dynamic characteristics (setup actually used)
- Equipment.png:
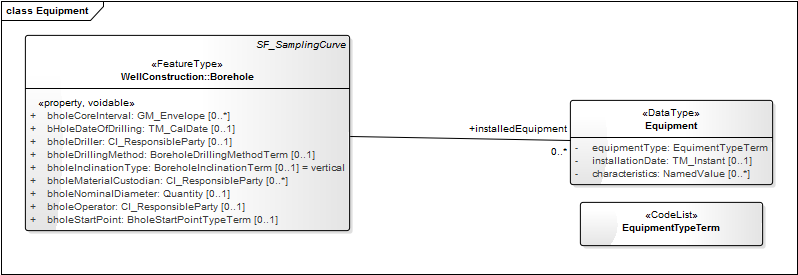
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
Equipment.png | manage | 27 K | 05 Feb 2015 - 17:50 | EricBoisvert | |
| |
TestEvent.png | manage | 59 K | 05 Feb 2015 - 14:37 | EricBoisvert | Aquifer Test |
| |
aquifertesting.png | manage | 104 K | 05 Feb 2015 - 13:58 | EricBoisvert | |
| |
layout_pump_test.png | manage | 85 K | 24 Feb 2015 - 18:04 | EricBoisvert | layout of the pumping test instance |
Edit | Attach | Print version | History: r4 < r3 < r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r4 - 24 Feb 2015, EricBoisvert
- Webs
-
 AIP8
AIP8
-
 ASTROdwg
ASTROdwg
-
 AgricultureSummit
AgricultureSummit
-
 AustraliaNewZealandForum
AustraliaNewZealandForum
-
 AviationDWG
AviationDWG
-
 BigDataDwg
BigDataDwg
-
 BusinessValueCommittee
BusinessValueCommittee
-
 CATdiscuss
CATdiscuss
-
 CDBswg
CDBswg
-
 CRSdefinitionResolver
CRSdefinitionResolver
-
 CRSdwg
CRSdwg
-
 CanadaForum
CanadaForum
-
 ChinaForum
ChinaForum
-
 CitSciIE
CitSciIE
-
 CitizenScienceDWG
CitizenScienceDWG
-
 ClimateChallenge2009
ClimateChallenge2009
-
 CoveragesDWG
CoveragesDWG
-
 DiscreteGlobalGridSystemsDWG
DiscreteGlobalGridSystemsDWG
-
 EMSpectrumDWG
EMSpectrumDWG
-
 EMspectrumDWG
EMspectrumDWG
-
 ERGuidance
ERGuidance
-
 EUforum
EUforum
-
 EarthCube
EarthCube
-
 EnergyUtilitiesDwg
EnergyUtilitiesDwg
-
 GML
GML
-
 GeoSciMLswg
GeoSciMLswg
-
 GeoScienceDWG
GeoScienceDWG
-
 GeocodingAdHoc
GeocodingAdHoc
-
 Geospatial3DMS
Geospatial3DMS
-
 HealthDWG
HealthDWG
-
 HydrologyDWG
HydrologyDWG
-
 I15swg
I15swg
-
 ILAFpublic
ILAFpublic
-
 ISGdwg
ISGdwg
-
 Ideas4OGC
Ideas4OGC
-
 JAG
JAG
-
 JSONsubGroup
JSONsubGroup
-
 JapanAssistance
JapanAssistance
-
 LandAdminDWG
LandAdminDWG
-
 MLSdwg
MLSdwg
-
 Main
Main
-
 MarineDWG
MarineDWG
-
 MassMarket
MassMarket
-
 MetOceanDWG
MetOceanDWG
-
 NREwg
NREwg
-
 NetCDFu
NetCDFu
-
 NordicForum
NordicForum
-
 OGC
OGC
-
 PointCloudDWG
PointCloudDWG
-
 QualityOfService
QualityOfService
-
 SWEProCitSci
SWEProCitSci
-
 Sandbox
Sandbox
-
 SmartCitiesDWG
SmartCitiesDWG
-
 System
System
-
 TemporalDWG
TemporalDWG
-
 UKIAP2013
UKIAP2013
-
 UrbanPlanningDWG
UrbanPlanningDWG
-
 Vocabulary
Vocabulary
-
 WCTileServiceSWG
WCTileServiceSWG
-
 WPS
WPS
-
 WaterML
WaterML
 The information you supply is used for OGC purposes only. We will never pass your contact details to any third party without your prior consent.
The information you supply is used for OGC purposes only. We will never pass your contact details to any third party without your prior consent. If you enter content here you are agreeing to the OGC privacy policy.
Copyright &© by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Ideas, requests, problems regarding OGC Public Wiki? Send feedback


